Overview

GameMaker has several facilities for performing object-to-object collision detection and response. This works great for dynamic actors within a game. Many games, however, employ statically defined tile maps for level assets which do not move. Just because something in a level is static, doesn’t mean it can’t be collided with! Unfortunately, GameMaker does not provide functions for performing collision checking against tile maps. This tutorial will focus on ray-to-tile collision checking.

The use cases for a ray-to-tile collision check are plenty:

Potential movement of an actor to a destination
Projectile collision checking
Visibility checks between objects (obstructed by a wall?)

tldr;

Don’t want to read through all the code and would rather just see the cool demo? Skip to the end!

Digital Differential Analyzer (DDA)

The DDA algorithm provides an elegant solution for ray casting in 2D space. A highly cited example of implementing the DDA algorithm can be fond on Lode Vandevenne’s page here.

Another fantastic reference on learning the DDA algorithm is this video from OneLoneCoder.

The tldr on the algorithm is this: Given a ray (or segment), walk along that ray, checking for intersections with locations in a grid.

But at this point some of you are asking: “Are you suggesting just sitting in a loop and slowly looping pixel-by-pixel towards the endpoint?”. Absolutely not! Not only would that implementation be insanely slow, but detecting the exact intersection point between the ray and a tile isn’t possible unless the loop step size is pixel-based - again, insanely slow!

What the DDA algorithm gives us is the ability to move along a ray in a unit direction - a tile - rather than some arbitrary per-step pixel amount. The speedup here is enormous.

GML Implementation

For our example, we’re going to create a simple function which takes a segment starting point, the segment endpoint, and the ID of a tile map to test against. Throughout this implementation you will see variable names with “ray” in them. While we’re technically working with segments, “ray” just fits nicer as a variable!

function TileRaycast(_x, _y, _rx, _ry, _map)

The return value from this function is a structure with information about the search operation

return {
	Found: tileFound,
	X: _endX,
	Y: _endY,
	Length: round(currentDistance * _tile_size),
	TileX: _stepX,
	TileY: _stepY		
}

Parameter	Description
Found	Boolean indicating if a tile was hit.
X	World X-coordinate of segment->tile intersection
Y	World Y-coordinate of segment->tile intersection
Length	Length of segment from starting point to collision point
TileX	Integer-based X-position of the tile within the tile map that was intersected
TileY	Integer-based Y-position of the tile within the tile map that was intersected

Implementation

function TileRayCast(_x, _y, _rx, _ry, _map) {
		
	// The assumption here is that tiles are always square!
	var _tile_size = tilemap_get_tile_width(_map);

	// Angle of the ray	
	var _rayDirectionX = _rx - _x;
	var _rayDirectionY = _ry - _y;
	var _rayLength = sqrt((_rayDirectionX * _rayDirectionX) + (_rayDirectionY * _rayDirectionY));	

	// Normalize the ray direction
	var _rayDirectionXNorm = _rayDirectionX / _rayLength;
	var _rayDirectionYNorm = _rayDirectionY / _rayLength;

	// Compute the ray step size in each direction (in tiles)
	// 2 == 2 tiles, not 2 pixels
	var _rayStepSizeX = sqrt(1.0 + (_rayDirectionYNorm / _rayDirectionXNorm) * (_rayDirectionYNorm / _rayDirectionXNorm));
	var _rayStepSizeY = sqrt(1.0 + (_rayDirectionXNorm / _rayDirectionYNorm) * (_rayDirectionXNorm / _rayDirectionYNorm));	

	// Determines in which direction in the tile map the algorightm will step.
	// Left = -1 | Right = 1 | Up = -1 | Down = 1
	var _stepX, _stepY;

	// Tracks the overall length of the ray, in tile units
	var _rayLengthX, _rayLengthY;
	
	// These track the integer grid position that the algorithm is currently in.
	// Example values if going in the top left tile and going directly to the right: (0,0 -> 1,0 -> 2,0)
	var _mapCheckX = _x div _tile_size;
	var _mapCheckY = _y div _tile_size;
	
	// Setup the ray step direction (sign) and the initial ray length.
	// The initial ray length isn't 0 because it's snapped to the AABB of each tile
	if(_rayDirectionXNorm < 0) {
		_stepX = -1;
		_rayLengthX = (_x - (_mapCheckX * _tile_size)) / _tile_size * _rayStepSizeX;	
	} else {
		_stepX = 1;
		_rayLengthX = (((_mapCheckX + 1) * _tile_size) - _x) / _tile_size *_rayStepSizeX;		
	}

	// Do the same for the Y-axis movement
	if(_rayDirectionYNorm < 0) {
		_stepY = -1;
		_rayLengthY = (_y - (_mapCheckY * _tile_size)) / _tile_size * _rayStepSizeY;	
	} else {
		_stepY = 1;
		_rayLengthY = (((_mapCheckY + 1) * _tile_size) - _y) / _tile_size *_rayStepSizeY;	
	}

	// Will become true IF a tile is found before the end of the line
	var tileFound = false;

	// The maximum distance of the ray, in tiles
	var maxDistance = _rayLength / _tile_size;

	// Algorithm's current distance, in tiles
	var currentDistance = 0.0;	

	// Start stepping!
	while(!tileFound && currentDistance < maxDistance) {
	
		// Walk along the shortest path
		if(_rayLengthX < _rayLengthY) {
			_mapCheckX += _stepX;
			
			currentDistance = _rayLengthX;			
			_rayLengthX += _rayStepSizeX;
		} else {
			_mapCheckY += _stepY;
			
			currentDistance = _rayLengthY;			
			_rayLengthY += _rayStepSizeY;
		}
	
		// Short circuit out if we've gone past _rx,_ry
		if(currentDistance >= maxDistance) {
			currentDistance = maxDistance;
			break;
		}		

		// Test tile at new test point
		if(tilemap_get(_map, _mapCheckX, _mapCheckY)) {
			tileFound = true;		
		}	
	}
	
	// Cap the distance to the maximum ray distance (start point - end point)
	if(currentDistance > maxDistance) 
		currentDistance = maxDistance;	
	
	// Translate the line end point from tile space into pixel coordinate space
	var _endX = _x + (_rayDirectionXNorm * (currentDistance * _tile_size));
	var _endY = _y + (_rayDirectionYNorm * (currentDistance * _tile_size));	
	
	return {
		Found: tileFound,
		X: _endX,
		Y: _endY,
		Length: round(currentDistance * _tile_size),
		TileX: _stepX,
		TileY: _stepY		
	}
} // end of TileRayCast()

“Break it down now…”

Let’s do a quick rundown of what the function is doing and dive into some of the more non-intuitive sections.

First thing first - figure out how big the tiles are. ASSUMPTION ALERT: tiles are assumed to be square.

var _tile_size = tilemap_get_tile_width(_map);

Figure out the direction (positive or negative) for each axis of the segment, as well as its length.

var _rayDirectionX = _rx - _x;
var _rayDirectionY = _ry - _y;
var _rayLength = sqrt((_rayDirectionX * _rayDirectionX) + (_rayDirectionY * _rayDirectionY));

Normalize each axis.

var _rayDirectionXNorm = _rayDirectionX / _rayLength;
var _rayDirectionYNorm = _rayDirectionY / _rayLength;

Calculate the ray step size (in tile integer space) on each axis

var _rayStepSizeX = sqrt(1.0 + (_rayDirectionYNorm / _rayDirectionXNorm) * (_rayDirectionYNorm / _rayDirectionXNorm));
var _rayStepSizeY = sqrt(1.0 + (_rayDirectionXNorm / _rayDirectionYNorm) * (_rayDirectionXNorm / _rayDirectionYNorm));	

Define some temporary variables that will be used within the main loop

// Determines in which direction in the tile map the algorightm will step.
// Left = -1 | Right = 1 | Up = -1 | Down = 1
var _stepX, _stepY;

// Tracks the overall length of the ray, in tile units
var _rayLengthX, _rayLengthY;

// These track the integer grid position that the algorithm is currently in.
// Example values if going in the top left tile and going directly to the right: (0,0 -> 1,0 -> 2,0)
var _mapCheckX = _x div _tile_size;
var _mapCheckY = _y div _tile_size;

// Will become true IF a tile is found before the end of the line
var tileFound = false;

// The maximum distance of the ray, in tiles
var maxDistance = _rayLength / _tile_size;

// Algorithm's current distance, in tiles
var currentDistance = 0.0;

// Track the total number of steps that the algorithm took
var _totalSteps = 0;

The next part determines the initial step direction and ray length. Remember, each step only moves on a single axis. In addition, the initial segment length is set so that the loop always starts on the edge of a tile.

if(_rayDirectionXNorm < 0) {
	_stepX = -1;
	_rayLengthX = (_x - (_mapCheckX * _tile_size)) / _tile_size * _rayStepSizeX;	
} else {
	_stepX = 1;
	_rayLengthX = (((_mapCheckX + 1) * _tile_size) - _x) / _tile_size *_rayStepSizeX;		
}

if(_rayDirectionYNorm < 0) {
	_stepY = -1;
	_rayLengthY = (_y - (_mapCheckY * _tile_size)) / _tile_size * _rayStepSizeY;	
} else {
	_stepY = 1;
	_rayLengthY = (((_mapCheckY + 1) * _tile_size) - _y) / _tile_size *_rayStepSizeY;	
}

At this point, it’s time to begin the main loop of the algorithm. Each iteration through the loop is considered a “step” in DDA parlance. The loop will continue until one of two conditions are met: 1) A tile is intersected 2) The current traveled segment distance is greater than the maximum distance specified by the parameters

Now let’s enter the loop…

Advance the current distance on whichever axis is shorter. Remember, _mapCheckX/Y tracks the tile index, in integer space.

if(_rayLengthX < _rayLengthY) {
	_mapCheckX += _stepX;
	
	currentDistance = _rayLengthX;			
	_rayLengthX += _rayStepSizeX;
} else {
	_mapCheckY += _stepY;
	
	currentDistance = _rayLengthY;			
	_rayLengthY += _rayStepSizeY;
}

In case the next step moves us past the maximum distance - bail!

if(currentDistance >= maxDistance) {
	currentDistance = maxDistance;
	break;
}

Check the tile map at the current location to see if there is a tile defined

if(tilemap_get(_map, _mapCheckX, _mapCheckY)) {
	tileFound = true;		
} 

Lastly, keep track of the number of steps that we’ve iterated through

_totalSteps++;

With the main loop complete, there is some housekeeping items to perform after the search is finished.

Translate the final end point from tile space into pixel space.

// Translate the line end point from tile space into pixel coordinate space
var _endX = _x + (_rayDirectionXNorm * (currentDistance * _tile_size));
var _endY = _y + (_rayDirectionYNorm * (currentDistance * _tile_size));

Return our findings to the caller!

return {
	Found: tileFound,
	X: _endX,
	Y: _endY,
	Length: round(currentDistance * _tile_size),
	TileX: _stepX,
	TileY: _stepY		
}

Debug Implementation

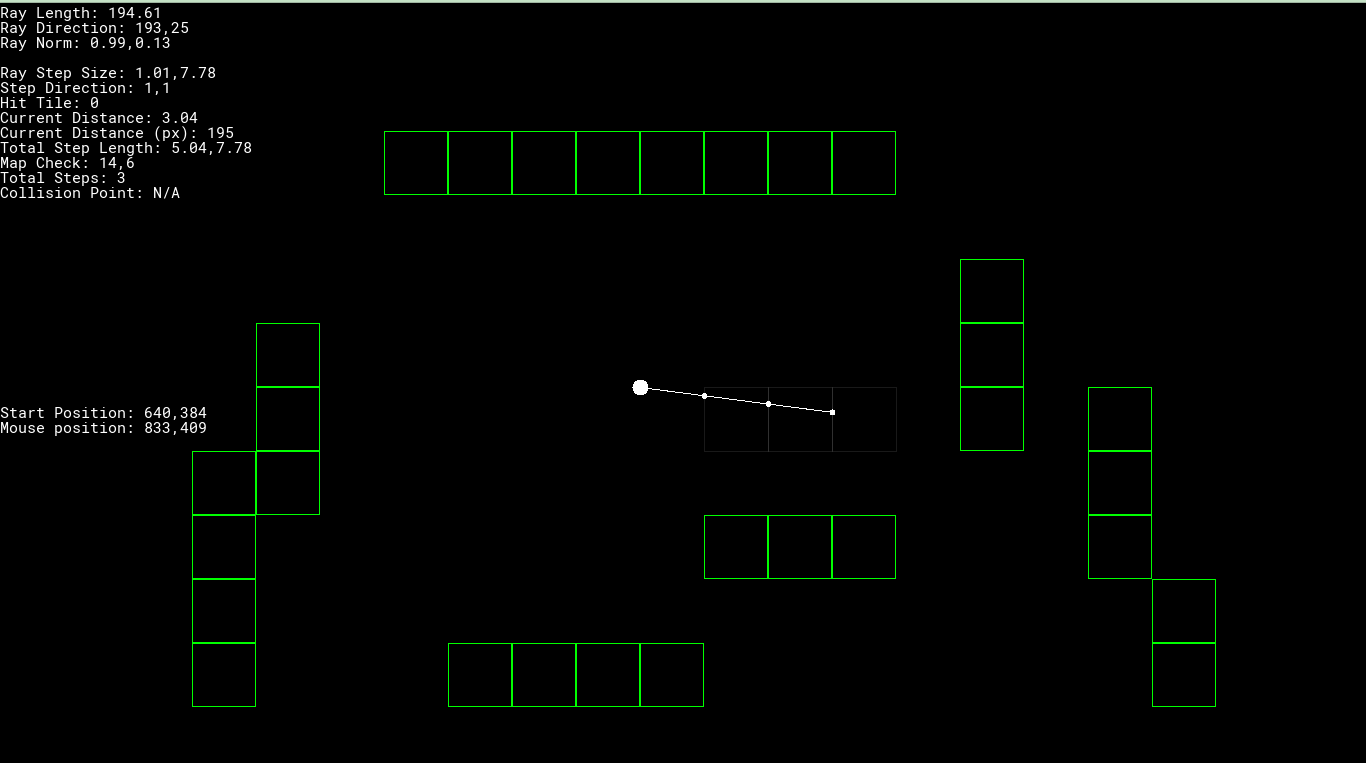
Of course, being able to visually see what is happening with the algorithm is one of the most useful ways to learn what is happening. In this version of the tile ray cast, debug output will be rendered to the screen. Information rendered includes:

Drawing the line segment
Text of all the relevant DDA algorithm variables (segment length, direction, normal, step size, step direction, etc)
“ghost outline” of tile map positions the segment passes through
dots where each iteration of the search loop occur (intersections of tile locations)
circle outline where an intersection with an existing tile occur

function TileRayCastDebug(_x, _y, _rx, _ry, _map) {
	
	// _x, _y, _rx, _ry, and _map will be passed into the function	
	draw_text(0, 400, "Start Position: " + string(_x) + "," + string(_y));
	draw_text(0, 415, "Mouse position: " + string(_rx) + "," + string(_ry));

	// The assumption here is that tiles are always square!
	var _tile_size = tilemap_get_tile_width(_map);

	// Angle of the ray	
	var _rayDirectionX = _rx - _x;
	var _rayDirectionY = _ry - _y;
	var _rayLength = sqrt((_rayDirectionX * _rayDirectionX) + (_rayDirectionY * _rayDirectionY));
	draw_text(0, 0, "Ray Length: " + string(_rayLength));
	draw_text(0, 15, "Ray Direction: " + string(_rayDirectionX) + "," + string(_rayDirectionY));

	// Normalize the ray direciton
	var _rayDirectionXNorm = _rayDirectionX / _rayLength;
	var _rayDirectionYNorm = _rayDirectionY / _rayLength;
	draw_text(0, 30, "Ray Norm: " + string(_rayDirectionXNorm) + "," + string(_rayDirectionYNorm));

	// Compute the ray step size in each direction (in tiles)
	// 2 == 2 tiles, not 2 pixels
	var _rayStepSizeX = sqrt(1.0 + (_rayDirectionYNorm / _rayDirectionXNorm) * (_rayDirectionYNorm / _rayDirectionXNorm));
	var _rayStepSizeY = sqrt(1.0 + (_rayDirectionXNorm / _rayDirectionYNorm) * (_rayDirectionXNorm / _rayDirectionYNorm));	
	draw_text(0, 60, "Ray Step Size: " + string(_rayStepSizeX) + "," + string(_rayStepSizeY));	

	// Determines in which direction in the tile map the algorightm will step.
	// Left = -1 | Right = 1 | Up = -1 | Down = 1
	var _stepX, _stepY;

	// Tracks the overall length of the ray, in tile units
	var _rayLengthX, _rayLengthY;
	
	// These track the integer grid position that the algorithm is currently in.
	// Example values if going in the top left tile and going directly to the right: (0,0 -> 1,0 -> 2,0)
	var _mapCheckX = _x div _tile_size;
	var _mapCheckY = _y div _tile_size;
	
	// Setup the ray step direction (sign) and the initial ray length.
	// The initial ray length isn't 0 because it's snapped to the AABB of each tile
	if(_rayDirectionXNorm < 0) {
		_stepX = -1;
		_rayLengthX = (_x - (_mapCheckX * _tile_size)) / _tile_size * _rayStepSizeX;	
	} else {
		_stepX = 1;
		_rayLengthX = (((_mapCheckX + 1) * _tile_size) - _x) / _tile_size *_rayStepSizeX;		
	}

	// Do the same for the Y-axis movement
	if(_rayDirectionYNorm < 0) {
		_stepY = -1;
		_rayLengthY = (_y - (_mapCheckY * _tile_size)) / _tile_size * _rayStepSizeY;	
	} else {
		_stepY = 1;
		_rayLengthY = (((_mapCheckY + 1) * _tile_size) - _y) / _tile_size *_rayStepSizeY;	
	}

	draw_text(0, 75, "Step Direction: " + string(_stepX) + "," + string(_stepY));

	// Will become true IF a tile is found before the end of the line
	var tileFound = false;

	// The maximum distance of the ray, in tiles
	var maxDistance = _rayLength / _tile_size;

	// Algorithm's current distance, in tiles
	var currentDistance = 0.0;
	
	// Track the total number of steps that the algorithm took
	var _totalSteps = 0;

	// Start stepping!
	while(!tileFound && currentDistance < maxDistance) {
	
		// Walk along the shortest path
		if(_rayLengthX < _rayLengthY) {
			_mapCheckX += _stepX;
			
			currentDistance = _rayLengthX;			
			_rayLengthX += _rayStepSizeX;
		} else {
			_mapCheckY += _stepY;
			
			currentDistance = _rayLengthY;			
			_rayLengthY += _rayStepSizeY;
		}
	
		// Short circuit out if we've gone past _rx,_ry
		if(currentDistance >= maxDistance) {
			currentDistance = maxDistance;
			break;
		}
	
		// Draw a dot where the current step finished at.
		var _tmpX = _x + (_rayDirectionXNorm * (currentDistance * _tile_size));
		var _tmpY = _y + (_rayDirectionYNorm * (currentDistance * _tile_size));
		draw_circle(_tmpX, _tmpY, 3, false);

		// Test tile at new test point
		if(tilemap_get(_map, _mapCheckX, _mapCheckY)) {
			tileFound = true;		
		} else {
			
			// Draw a "ghost tile" representing the tile that was tested against
			var _tmpX = _mapCheckX * _tile_size;
			var _tmpY = _mapCheckY * _tile_size;
			
			draw_set_color(c_white);
			draw_set_alpha(0.1);
			draw_rectangle(_tmpX, _tmpY, _tmpX + _tile_size, _tmpY + _tile_size, true);
			
			// Reset the alpha 
			draw_set_alpha(1.0);
		}
	
		_totalSteps++;
	}
	
	// Cap the distance to the maximum ray distance (start point - end point)
	if(currentDistance > maxDistance) 
		currentDistance = maxDistance;
	
	draw_text(0, 90, "Hit Tile: " + string(tileFound));
	draw_text(0, 105, "Current Distance: " + string(currentDistance));
	draw_text(0, 120, "Current Distance (px): " + string(round(currentDistance * _tile_size)));
	
	draw_text(0, 135, "Total Step Length: " + string(_rayLengthX) + "," + string(_rayLengthY));
	draw_text(0, 150, "Map Check: " + string(_mapCheckX) + "," + string(_mapCheckY));
	draw_text(0, 165, "Total Steps: " + string(_totalSteps));
	
	// Translate the line end point from tile space into pixel coordinate space
	var _endX = _x + (_rayDirectionXNorm * (currentDistance * _tile_size));
	var _endY = _y + (_rayDirectionYNorm * (currentDistance * _tile_size));

	if(tileFound) {
		draw_text(0, 180, "Collision Point: " + string(_endX) + "," + string(_endY));
		draw_circle(_endX, _endY, 10, true);
	} else {
		draw_text(0, 180, "Collision Point: N/A");
	}

	draw_line(_x, _y, _endX, _endY);
	
	return {
		Found: tileFound,
		X: _endX,
		Y: _endY,
		Length: round(currentDistance * _tile_size),
		TileX: _stepX,
		TileY: _stepY		
	}
} // end of TileRayCastDebug()

Live Demo

I’ve created a live demo for you to see the DDA algorithm in action. The complete source code for the GameMaker project is available here. In the demo, simply move your mouse anywhere in the viewport to change the endpoint of the segment. Use the arrow keys on your keyboard to move the starting point of the segment.

Enjoy!